

| multiplo di p | 6 | 12 | 18 | 24 | 30 |
|---|---|---|---|---|---|
| multiplo di q | 15 | 15 | 15 | 30 | 30 |
Si è visto che l'algoritmo euclideo è il più efficiente per calcolare M.C.D. e m.c.m. tra due o più numeri. La tabella a destra mostra la traccia dell'algoritmo per i due numeri p=6 e q=15.
Questo algoritmo si ferma sempre, quali che siano i due numeri, infatti nella peggiore delle ipotesi, quella che p e q siano primi tra di loro, si fermerà quando si raggiunge il prodotto pq.
Ma cosa accadrebbe se invece di cominciare da zero si cominciasse da due qualsiasi numeri interi positivi a e b? L'algoritmo si fermerebbe sempre o no?
| p | 1 | 7 | 13 | 19 | 19 | 25 | 31 | 37 | 37 | 43 | 49 | 55 | 61 | 67 ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q | 3 | 18 | 18 | 18 | 33 | 33 | 33 | 33 | 48 | 48 | 48 | 63 | 63 | 63 ... |
Basta un controesempio con a = 1 e b = 3 per convincersi che l'arresto non è più garantito.
Perchè avviene questo? Il motivo è evidente: avendo i due numeri 6 e 15 un fattore comune, il 3 (M.C.D. tra 6 e 15), la prima serie che comincia da 1 genera comunque numeri del tipo 3n+1 (o anche 6n +1), cioè maggiori di uno dei multipli del 3; la seconda che comincia da 3 genera solo multipli del tre! In pratica è come se le due serie corressero su due binari paralleli che non si incontreranno mai! Più in generale le due serie possono correre su 3 binari separati: 1) i multipli del tre (3n); 2) i multipli del 3 aumentati di 1 (3n+1); 3) i multipli del 3 aumentati di 2 (3n+2). Il numero di binari separati è chiaramente pari al M.C.D. tra p e q.
| mult. p | 10 | 10 | 20 | 20 | 30 | 30 | 30 | 40 | 40 | 50 | 50 | 50 | 60 | 60 | 70 | 70 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mult. q | 7 | 14 | 14 | 21 | 21 | 28 | 35 | 35 | 42 | 42 | 49 | 56 | 56 | 63 | 63 | 70 |
Però se i due numeri p e q sono primi tra di loro, allora l'arresto è di nuovo garantito. Per esempio per calcolare il m.c.m. tra 10 e 7, che sono appunto primi tra di loro, si ha la tavola di traccia a destra che dà m.c.m. = 70.
| p | 1 | 11 | 11 | 11 | 21 | 21 | 31 | 31 |
|---|---|---|---|---|---|---|---|---|
| q | 3 | 3 | 10 | 17 | 17 | 24 | 24 | 31 |
Partendo di nuovo da a = 1 e b = 3 si ha invece la tabella a destra che trova un numero comune 31.
Infatti essendo 1 il M.C.D. tra 7 e 10, il numero di binari è 1, le due serie corrono sullo stesso binario e periodicamente, con periodo pq (qui 70) ci sarà un numero comune, in questo caso 31, 101, 171 ...
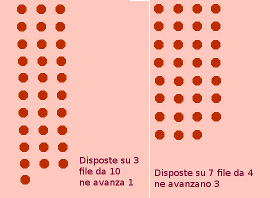
Il disegno a lato illustra in altro modo il problema: supponendo di avere 31 monete, queste possono disporsi su 10 file, ma ne avanza 1; oopure su 7 file ma ne avanzano 3.
Altre combinazioni possono essere provate nella pagina interattiva su questo teorema.
Questo risultato in buona sostanza costiuisce il famoso e antichissimo teorema cinese del resto, così detto perchè il primo enunciato è dovuto a Sun Zi matematico cinese del III secolo d.C.
Usando la notazione delle aritmetiche finite può essere enunciato così:
Detto in altre parole: dati due numeri primi tra di loro p e q, e due numeri interi qualsiasi a e b esiste sempre un x che diviso per p dia resto a e diviso per q dia resto b. Di qui il nome di teorema del resto.
Come l'algoritmo del m.c.m. questo teorema si estende anche a più di due numeri, e si può riformulare così: Dati n numeri primi tra di loro p1, p2 ... pn, ed n numeri qualsiasi a1, a2 ... an esiste sempre un x tale che:
x = a1 mod p1
x = a2 mod p2
...
x = an mod pn
Come appare evidente l'algoritmo euclideo può essere adattato anche per calcolare questo valore x.
Tornando all'esempio delle monete, e supponendo di non conoscerne il numero totale, il teorema del resto può calcolare il numero di monete senza contarle tutte, ma solo contando i resti disponendole su diversi numeri di file. Così se si dispongono N monete su 7 file e ne avanzano 3, e poi si dispongono su 10 file e ne avanza 1, si tratta di risolvere il sistema:
x = 3 mod 7
x = 1 mod 10
Il teorema cinese del resto con l'algoritmo euclideo consente di calcolare la prima soluzione del problema, che è appunto 31.
Il teorema cinese del resto è importante anche in crittografia; infatti il cifrario RSA deve fare calcoli modulo pq, dove p e q sono due numeri primi molto grandi (1024 o 2048 bit) e le operazioni modulari con modulo così grande richiedono tempi molto lunghi. Il teorema del resto permette di fare i calcoli in modulo p e q con una sensibile riduzione dei tempi.
Il metodo può essere provato alla pagina PhP sul prodotto di due numeri in aritmetica modulare.