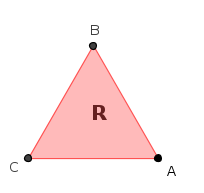
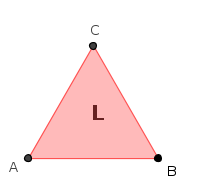
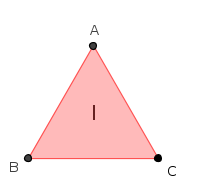
L'insieme delle tre rotazioni di un triangolo equilatero su se stesso con l'operazione di composizione delle rotazioni (una rotazione seguita da un'altra rotazione) costituisce un gruppo commutativo che chiameremo RT; le tre rotazioni possibili sono:
| I | L | R | |
|---|---|---|---|
| I | I | L | R |
| L | L | R | I |
| R | R | I | L |
I è l'elemento neutro, R ed L sono l'uno l'inverso dell'altro; infatti RL = LR = I. A lato la tavola di moltiplicazione del gruppo.
Inoltre R2 = L e L2 = R mentre ovviamente R3 = L3 = I (con tre rotazioni si torna alla posizione di partenza).
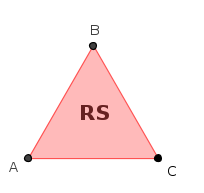
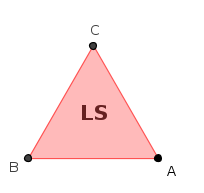
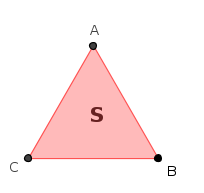
L'insieme delle isometrie di un triangolo equilatero ABC su se stesso e l'operazione di composizione delle isometrie (una seguita da un'altra) costituisce un gruppo non commutativo; alle tre rotazioni del gruppo precedente si aggiungono i tre ribaltamenti del triangolo sulle sue tre altezze.
Il ribaltamento del triangolo rispetto all'altezza da A si chiamerà S. Gli altri due ribaltamenti vengono chiamati RS ed LS, infatti equivalgono ad una rotazione seguita da S.
| I | L | R | S | LS | RS | |
|---|---|---|---|---|---|---|
| I | I | L | R | S | LS | RS |
| L | L | R | I | LS | RS | S |
| R | R | I | L | RS | S | LS |
| S | S | RS | LS | I | R | L |
| LS | LS | S | RS | L | I | R |
| RS | RS | LS | S | R | L | I |
Come sopra I è l'elemento neutro, R, L sono tutti l'uno l'inverso dell'altro; invece S, RS, LS sono l'inverso di se stessi; per esempio RSRS = RLSS = II = I. A lato la tavola di moltiplicazione del gruppo che non è abeliano (commutativo). Si nota in particolare che che RS = SL e LS = SR.
Il gruppo iniziale RT ne è sottogruppo ed ha due classi laterali: S.RT e RT.S
Questo sito non fa uso di cookies propri. Possono peraltro essere presenti cookies di terze parti.
Pagina a cura di Paolo Bonavoglia (paolo@bonavoglia.eu) del